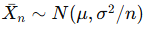티스토리 뷰
Q. 중심극한정리는 왜 유용한걸까요?
1. 중심극한정리(Central Litmit Theorem, CLT) 란?
- 모집단이 어떤 분포를 따르든 충분히 큰 크기의 표본을 여러번 추출하여 그 표본 평균을 구하면, 그 표본 평균의 분포는 정규분포에 가까워진다.
2. 중심극한정리의 활용성
- 많은 통계 기법이 정규분포를 가정하고 설계되어 있다. (t-검정, 회귀분석, 신뢰구간 계산 등)
- 정규분포를 근사적으로 사용할 수 있는 근거를 제공해 통계적 추론을 수행할 수 있다.(분석의 정당성 확보)
- 데이터를 정규분포로 근사함으로써 실직적인 문제 해결에 도움을 준다.
- 예시: 공장에서 생산된 제품의 품질 데이터를 정규분포로 근사하여, 평균 품질을 분석하거나 결함률을 추정할 수 있다.
3. 중심극한정리의 가정
- 표본의 크기가 충분히 커야 한다.
- 표본이 독립적으로 추출되어야 한다.
- 모집단이 극단적으로 분산이 크거나 특이한 경우(무한히 긴 꼬리를 가진 분포 등), 표본의 크기가 매우 커야 한다.
2. 대수의 법칙
- 표본의 크기가 충분히 커지면, 표본 평균이 모집단의 기대값(평균)에 점점 가까워 진다.
- 표본 평균을 모집단 평균의 근사값으로 사용할 수 있어 표본 평균의 신뢰성을 보장(정확도가 높아짐)
- 통계적 추정의 이론적 기반(표본 평균으로 모집단 평균 추정)
3. 중심극한정리와 대수의 법칙
| 구분 | 대수의 법칙 | 중심극한정리 |
| 초점 | 표본 평균이 모집단 평균에 수렴 | 표본 평균의 분포가 정규분포에 가까워짐 |
| 역할 | 표본평균이 점추정값으로 적합하다는 것을 뒷받침 | 표본평균의 분포적 특성을 제공해 신뢰구간과 같은 구간추정을 가능하게 함 |
| 표현 |
1) 점추정: 모집단의 특정 값(평균, 분산 등)을 하나의 값으로 추정
예) 표본 평균으로 모집단의 평균을 추정
2) 구간추정: 모집단의 특정 값에 대한 범위(구간)을 제공하며, 이 구간이 참값을 포함할 확률(신뢰수준)을 명시
예) 신뢰구간으로 모집단 평균의 범위를 제시
'AI > 기술면접준비' 카테고리의 다른 글
| [기술면접] 정규화(Regularization), Lasso(L1 규제), Ridge(L2 규제) (0) | 2024.12.14 |
|---|---|
| [기술면접] 오차(Error)와 편향(Bias), 분산(Variance), 정규화(Regularization) (0) | 2024.12.13 |
| [기술면접] 엔트로피(entropy)와 Information Gain에 대해 설명해주세요. (1) | 2024.12.11 |
| [기술면접] 정규성(Normality) 검정 (2) | 2024.11.14 |
| [기술면접] 정규화(Normalization) (0) | 2024.11.13 |
- Total
- Today
- Yesterday
- 실기
- llm
- 고득점 Kit
- Python
- 다이어트
- 아침운동
- IH
- 미라클모닝
- Ai
- 습관
- opic
- 갓생
- 프로그래머스
- SQL
- 줄넘기
- 빅데이터 분석기사
- ChatGPT
- 30분
- 아침
- 루틴
- 운동
- 티스토리챌린지
- C언어
- 영어회화
- 경제
- 오픽
- 뉴스
- 스크랩
- 기초
- 오블완
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |