티스토리 뷰
※ 빅데이터 분석기사 실기 체험: 예제 풀어보기 https://dataq.goorm.io/exam/3/%EB%B9%85%EB%8D%B0%EC%9D%B4%ED%84%B0%EB%B6%84%EC%84%9D%EA%B8%B0%EC%82%AC-%EC%8B%A4%EA%B8%B0-%EC%B2%B4%ED%97%98/quiz/5
1. 타이타닉 데이터셋 다운로드: https://www.kaggle.com/c/titanic/
2. 문제풀이
1) Sex와 Survived 변수 간의 독립성 검정시 카이제곱 통계량은? (반올림하여 소수 셋째짜리 까지 계산)
import pandas as pd
import numpy as np
# 파일 불러오기
df= pd.read_csv('train_titanic.csv')
df.info()
# 결측치 확인
df['Sex'].isna().sum(), df['Survived'].isna().sum()
# (0, 0)
# 빈도표 생성
contingency_table = pd.crosstab(df['Sex'], df['Survived'])
contingency_table
# 카이제곱 검정
from scipy.stats import chi2_contingency
chi2, p_value, dof, expected = chi2_contingency(contingency_table)
print(np.round(chi2,3))
# 260.717
2) Sex와 SibSp, Parch, Fare를 독립변수를 사용하여 로지스틱 회귀모형을 실시하였을때, Parch변수의 계수값은?
(반올림하여 소수 셋째 자리까지 계산)
X = df[['Sex', 'SibSp','Parch','Fare']]
X.info()
# 문자형을 숫자형으로 변경
X['Sex'] = X['Sex'].map({'male':0, 'female':1})
X.info()
y = df['Survived']
# 로지스틱 회귀
import statsmodels.api as sm
X = sm.add_constant(X)
logit_model = sm.Logit(y, X)
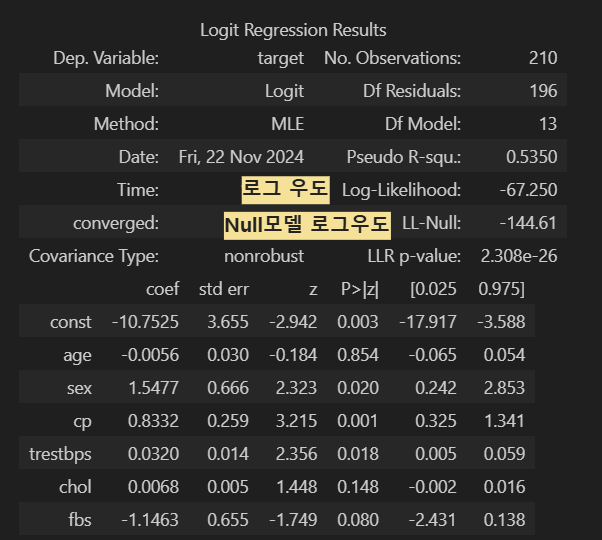
result = logit_model.fit()
print(result.summary())
print(np.round(result.params['Parch'],3))
#-0.201
3) 위 문제에서 추정된 로지스틱 회귀모형에서 SibSp변수가 한 단위 증가할 때 생존할 오즈비(Odds ratio)값은?
(반올림하여 소수 셋째 자리까지 계산)
print(np.round(np.exp(result.params['SibSp']),3))
# 0.702
* 오즈비 공식:

- Odds Ratio > 1 : 변수 증가가 사건 발생 확률을 높이는 경향이 있음
- Odds Ratio < 1 : 변수 증가가 사건 발생 확률을 낮추는 경향이 있음
- Odds Ratio = 1 : 변수 증가가 사건 발생 확률을 영향을 주지 않음
4) 로지스틱 회귀모델 예측결과는 확률로 나온다!
y_pred_prob = model.predict(X)
y_pred = (y_pred_prob>0.5).astype(int)
5) 오류율

3. 로지스틱 회귀모델
- 로그오즈(log-odds)를 선형 모델로 표현한 것

1) 오즈(Odds): 어떤 사건이 발생할 확률(P)과 발생하지 않을 확률 (1-P)의 비율

2) 오즈비(Odds Ratio): 한 변수의 값이 한 단위 증가할 때, 오즈가 얼마나 변하는지

4. 로짓 우도
- 로지스틱 회귀의 로그 우도(Log-Likelihood) [ Likelihood: 가능성 ]
1) 우도(Likelihood)란?
- 모델이 데이터를 얼마나 잘 설명하는지 "확률" 크기를 나타냄 (클수록 좋음)
- 각 데이터에서 실제 결과에 해당하는 예측 확률(1일 확률 또는 0일 확률)을 모두 곱한 값
- 확률의 곱이라서 데이터가 많아질수록 값이 작아져 계산이 어려워 로그우도를 주로 사용
- 이진 또는 확률 데이터에서 사용
- 음수나 지수화된 값
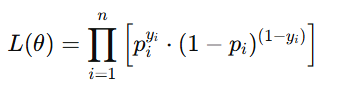
2) 로그 우도
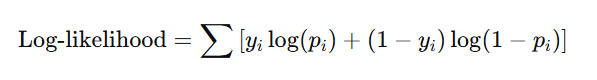
3) 최대우도 추정(MLE)
- Maximum Likelihood Estimation
- 관측된 데이터를 가장 잘 설명하는 회귀계수를 찾는 방법, 우도를 최대화하는회귀계수 값을 추정하는 과정
- 계산을 쉽게 하기 위해 로그우도로 계산한다.
5. 잔차이탈도 (Residual Deviance)
- 모델이 데이터를 얼마나 잘 설명하는지(작을수록 좋음)
- 이탈도(deviance): 예측값과 실제값의 오차
* (-2)는왜 곱할까?
- 로그우도는 음수거나 0에 가까운 값을 가져 -2를 곱하므로써 양수 값으로 변환하고, 로그스케일을 직관적으로 해석 가능
- 로그우도 "차이"에 -2를 곱하면 카이제곱 통계량과 유사한 형태를 가져, 두 모델이 통계적으로 유의미한 차이가 있는지 판단 할 수 있다.
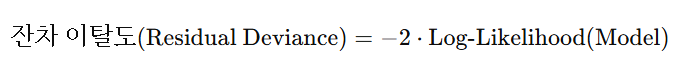
6. Null 이탈도
- Target의 평균만 사용해 예측한 모델의 설명력
- 목적: 독립변수를 사용하지 않은 기본 모델의 성능을 측정해 현재 모델의 성능 향상을 확인하기 위함
'AI > 빅데이터분석기사(통계)' 카테고리의 다른 글
| [빅데이터 분석기사 실기] 작업1유형 1.전처리 함수 (1) | 2024.11.23 |
|---|---|
| [빅데이터 분석기사 실기] 9회 실기 시험 준비(시험 환경 확인) (0) | 2024.11.20 |
| [빅데이터 분석기사 실기] 작업형3유형 1.통계적검정 (0) | 2024.11.19 |
| [빅데이터 분석기사 실기] 4회기출 작업형1유형 연습문제 풀이 (0) | 2024.11.17 |
| [빅데이터 분석기사 실기] 사분위수, 표준편차 (0) | 2024.07.10 |
- Total
- Today
- Yesterday
- 고득점 Kit
- 영어회화
- 다이어트
- 실기
- Python
- 갓생
- 빅데이터 분석기사
- 스크랩
- 미라클모닝
- 기초
- Ai
- IH
- 줄넘기
- SQL
- 뉴스
- 루틴
- 오픽
- ChatGPT
- 티스토리챌린지
- 30분
- 아침운동
- 경제
- 오블완
- 아침
- llm
- 프로그래머스
- 운동
- opic
- 습관
- C언어
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
